Bebras is an international initiative aiming to promote Informatics (Computer Science, or Computing) and computational thinking among school students at all ages. Participants are usually supervised by teachers who may integrate the Bebras challenge in their teaching activities. The challenge is performed at schools using computers or mobile devices.

Pupils of the HTBLuVA-Salzburg have proven their skills - and found an additional solution, that the creators of the original taks hadn't thought about. 

Task in German only.

Wie viele Wanderrouten sind möglich?

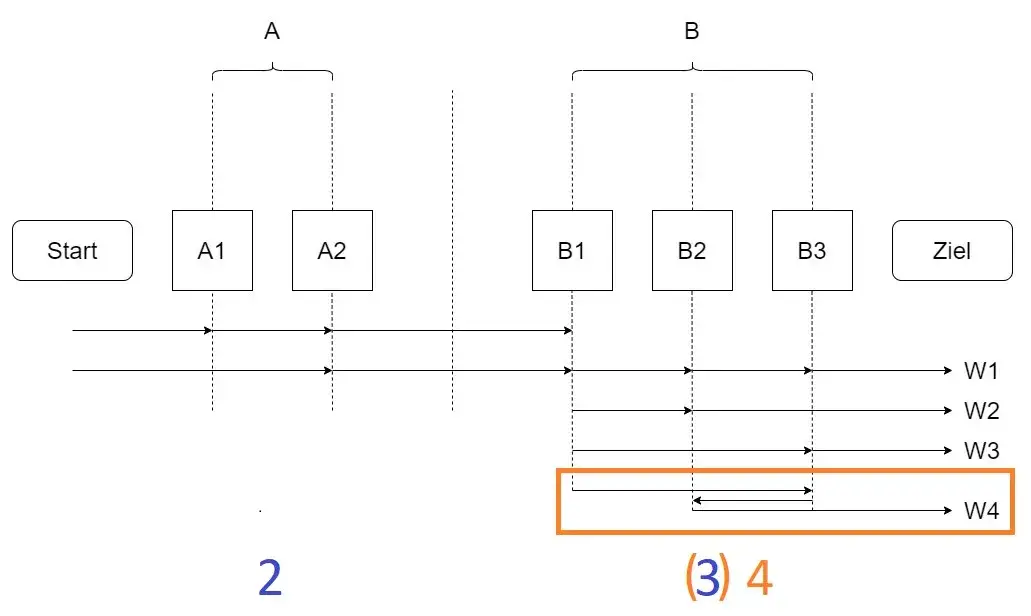
In der Aufgabe "Wanderungen" geht es um die Anzahl der möglichen Wanderrouten von einem Start- zu einem Zielpunkt (siehe folgende Abbildung).

Bevor Sie weiterlesen, können Sie gerne selbst versuchen, die Aufgabe zu lösen. Nehmen Sie sich ruhig etwas Zeit. Teilnehmende beim Biber-Wettbewerb haben dafür allerdings für jede Aufgabe nur wenige Minuten. 

Ein ganz wichtiger Punkt zur raschen Lösung der Aufgabe im Sinne der Problemzerlegung des Computational Thinking ist die Erkenntnis, dass man die vorderen und die hinteren Routen getrennt betrachten kann und das Ergebnis dann das Produkt der beiden Werte ist. 

Die offizielle Lösung lautet wie folgt: Mit 2 möglichen Routen im linken Teil der Strecke und 3 mögliche Routen im rechten Teil der Strecke, ergibt das (2*3 =) 6 mögliche Routen.

Im vorliegenden Fall hat sich jedoch eine weitere Lösung versteckt. Professor Fridolin Einböck, ein sehr engagierter Biber-Koordinator der renommierten HTBLuVA Salzburg, meldete sich mit folgender Skizze bei uns und machte uns auf die weitere Lösung aufmerksam.  

Was nicht ausgeschlossen ist, ist möglich

Die Sache ändert sich nämlich, wenn man erlaubt, dass Mia auch zurückgehen darf, dann sind es 8 mögliche Routen. Da die Option der Rückkehr nicht ausdrücklich ausgeschlossen war, muss diese Antwort als richtig gewertet werden, denn es ist zwar nicht unbedingt intuitiv, dass man bei einer Wanderung Teilstrecken wieder zurückgeht, aber das genügt nicht, um eine sonst gültige Lösung auszuschließen. 

Hier zeigt sich wieder: Eine wichtige Eigenschaft in der Informatik ist das genaue Beobachten und Erkennen von Details, die sich erst bei ganz genauer Betrachtung oder sogar erst bei einer praktischen Umsetzung ergeben.

Thank you to teacher Fridolin Einböck and his pupils of the HTBLuVA Salzburg for their crative skills and feedback!